FiveThirtyEight: The Riddler (2016-July-08)
I hate puzzles, but for some reason I find the Riddler from FiveThirtyEight more addicting than Flavor Blasted Goldfish. Anyway, I decided to post my solution for this week. Below is the question:
The archvillain Laser Larry threatens to imminently zap Riddler Headquarters (which, seen from above, is shaped like a regular pentagon with no courtyard or other funny business). He plans to do it with a high-powered, vertical planar ray that will slice the building exactly in half by area, as seen from above. The building is quickly evacuated, but not before in-house mathematicians move the most sensitive riddling equipment out of the places in the building that have an extra high risk of getting zapped.
Where are those places, and how much riskier are they than the safest spots? (It’s fine to describe those places qualitatively.)
Doesn’t seem too difficult right? Well first things first, lets create a pentagon about the origin [0,0] and calculate its area.
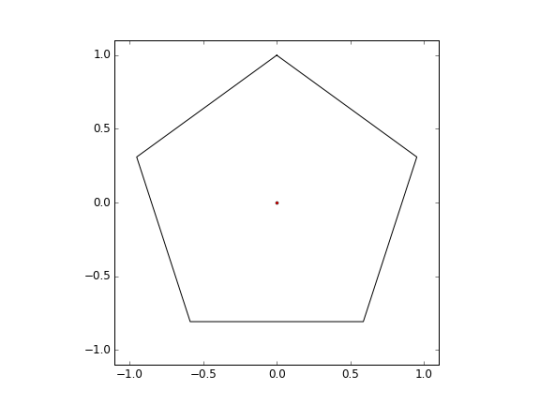
Using the length of one of its edges (a), we can calculate the total pentagon area using:
Since every edge
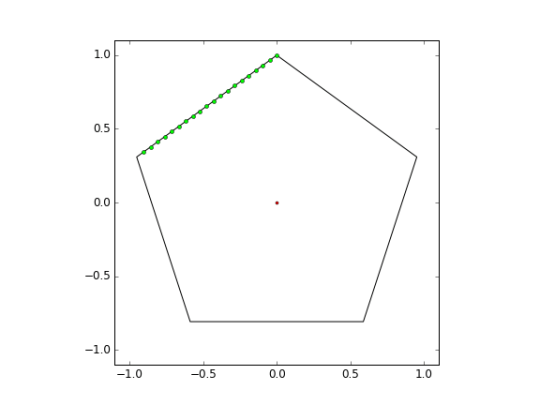
I only created twenty cut points, but this is only for visualization. I will bump that number up to several hundred for the final run.
Next we need to figure out where on the other sides of the pentagon the laser must cross in order to split the pentagon into two equal area halves.
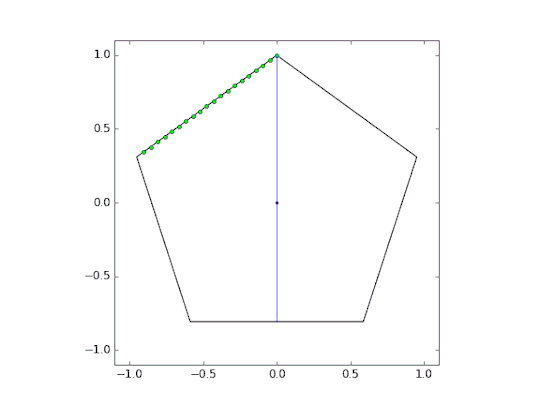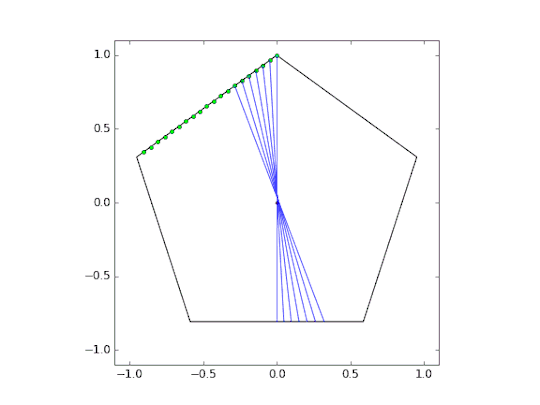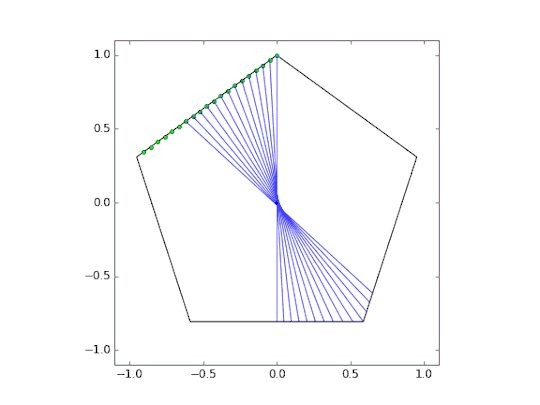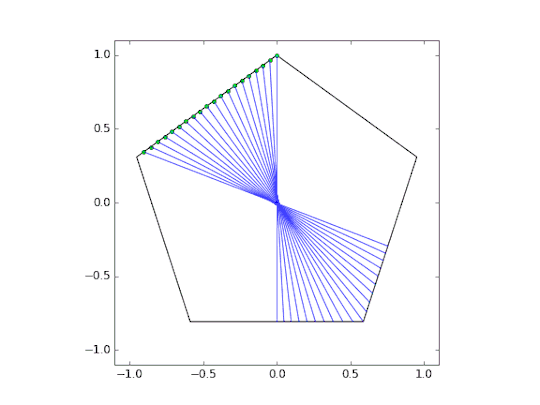
This was accomplished by creating a series of triangles and optimizing them using Powell’s method. The cost function for this optimization was simple; the area of the colored triangles must equal exactly one half of the total pentagon area. Below is a quick animation showing the optimization.
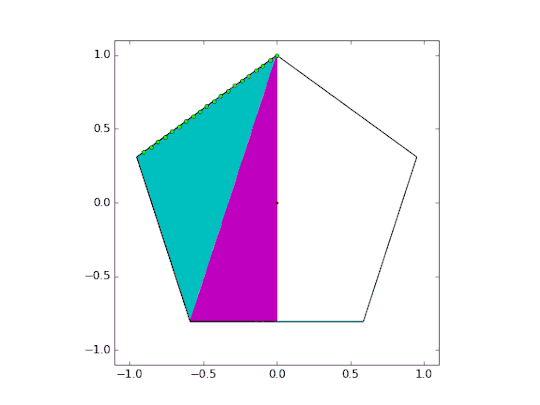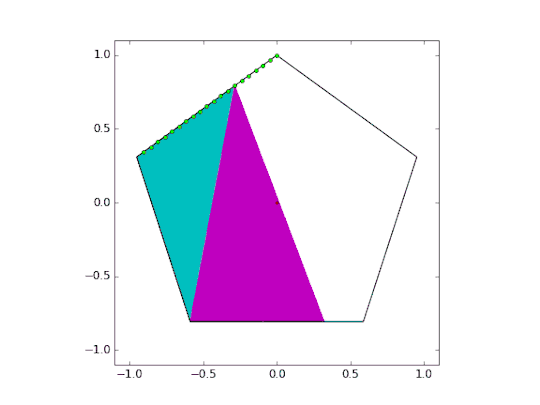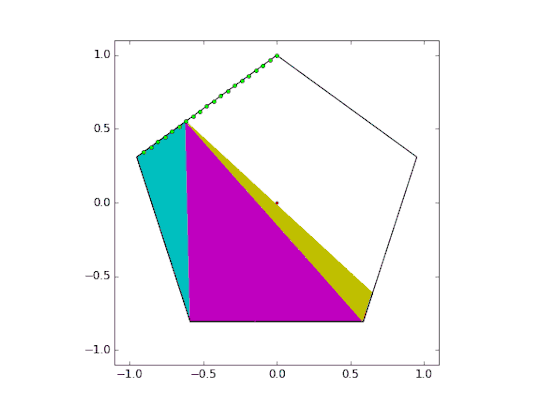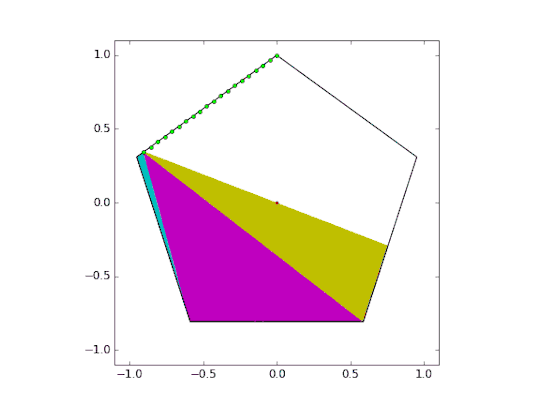
Now that the hard part is over, we can increase the number of cut points and lower the alpha channel.
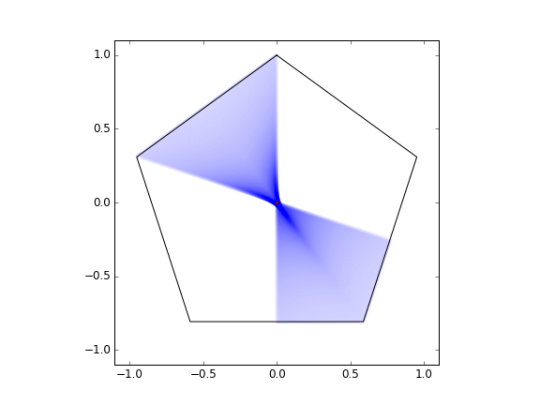
Rotating the results four more times about the origin results in the final solution seen below. The star pattern emerges because not every cut crosses the centroid of the pentagon.
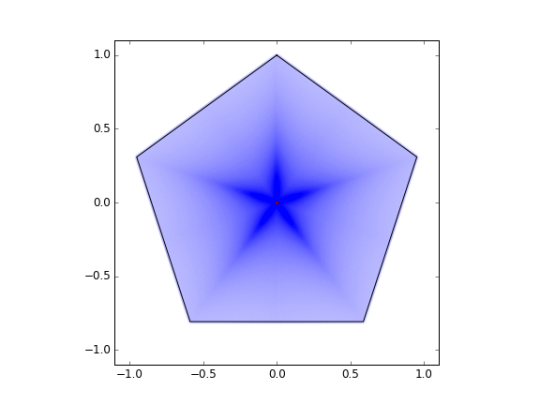
Darker areas represent locations where the laser is crossing more frequently. Therefore the equipment should be moved to the midpoint of each wall to minimize damage. I think…
Below is the code:
#------------------------------------------------------------------------------+
#
# The Riddler - July 8th, 2016
# FiveThirtyEight
#
#------------------------------------------------------------------------------+
#--- IMPORT DEPENDENCIES ------------------------------------------------------+
from __future__ import division
from matplotlib import pyplot as plt
from scipy.optimize import minimize
from math import sin,cos,radians,degrees,pi,sqrt
#------------------------------------------------------------------------------+
# create a pentagon centered @ [0,0]
angles=[i for i in range(90,450,72)]
pentagon_pts=[]
for i in range(len(angles)):
x=cos(radians(angles[i]))
y=sin(radians(angles[i]))
pentagon_pts.append([x,y])
# calculate total area based on length of one side
a=abs(pentagon_pts[2][0])+abs(pentagon_pts[3][0]) # length of bottom edge
area_total=0.25*sqrt(5.0*(5.0+2.0*sqrt(5.0)))*a**2 # total pentagon area
# create perimeter points (on single edge only)
num_cuts=200
delta_x=(pentagon_pts[1][0]-pentagon_pts[0][0])/num_cuts
delta_y=(pentagon_pts[1][1]-pentagon_pts[0][1])/num_cuts
cut_pts_x=[delta_x*i+pentagon_pts[0][0] for i in range(0,num_cuts)]
cut_pts_y=[delta_y*i+pentagon_pts[0][1] for i in range(0,num_cuts)]
def triangleArea(points):
x_a=points[0]
y_a=points[1]
x_b=points[2]
y_b=points[3]
x_c=points[4]
y_c=points[5]
area=0.5*abs((x_a-x_c)*(y_b-y_a)-(x_a-x_b)*(y_c-y_a))
return area
# simulate laser cuts
laser_cuts_x=[]
laser_cuts_y=[]
for i in range(len(cut_pts_x)):
triangle1_plot=[]
triangle2_plot=[]
triangle3_plot=[]
# cost function
def testFunc(x0):
#--- triangle #1 ----------------------------------+
area_tri_1=triangleArea([cut_pts_x[i],
cut_pts_y[i],
pentagon_pts[1][0],
pentagon_pts[1][1],
pentagon_pts[2][0],
pentagon_pts[2][1]])
#--- triangle #2 ----------------------------------+
area_tri_2=triangleArea([cut_pts_x[i],
cut_pts_y[i],
pentagon_pts[2][0],
pentagon_pts[2][1],
x0,
pentagon_pts[2][1]])
# check to make sure the new calculated piint is between the two bottom points
if x0>=pentagon_pts[2][0] and x0<=pentagon_pts[3][0]:
return abs((area_tri_1+area_tri_2)-(0.5*area_total))
# if the calculated point goes beyond the bottom right point, recalculate using three triangles
if x0>pentagon_pts[3][0]:
#--- recalculate triangle area #2 -------------+
area_tri_2=triangleArea([cut_pts_x[i],
cut_pts_y[i],
pentagon_pts[2][0],
pentagon_pts[2][1],
pentagon_pts[3][0],
pentagon_pts[3][1]])
#--- triangle #3 ------------------------------+
# calculate slope between points #3 and #4
del_y=pentagon_pts[4][1]-pentagon_pts[3][1]
del_x=pentagon_pts[4][0]-pentagon_pts[3][0]
slope=del_y/del_x
y_c=pentagon_pts[3][1]+((x0-pentagon_pts[3][0])*slope)
# calculate new area for triangle #3
area_tri_3=triangleArea([cut_pts_x[i],
cut_pts_y[i],
pentagon_pts[3][0],
pentagon_pts[3][1],
x0,
y_c])
# calculate new cost func
func=abs((area_tri_1+area_tri_2+area_tri_3)-(0.5*area_total))
return func
# if point is less than the bottom right edge
if x0<pentagon_pts[2][0]:
return 1
# optimize function to determine x_c
xopt=minimize(testFunc,0,method='Powell',options={'disp':False,'ftol': 1e-10,'maxiter':1000})
print xopt.x
if pentagon_pts[2][0]<=xopt.x and xopt.x<=pentagon_pts[3][0]:
y_c=pentagon_pts[2][1]
if xopt.x>pentagon_pts[3][0]:
del_y=pentagon_pts[4][1]-pentagon_pts[3][1]
del_x=pentagon_pts[4][0]-pentagon_pts[3][0]
slope=del_y/del_x
y_c=pentagon_pts[3][1]+((xopt.x-pentagon_pts[3][0])*slope)
# save results
laser_cuts_x.append(xopt.x)
laser_cuts_y.append(y_c)
# rotate results 72 degrees, four times about orgin [0,0]
def rotate(x,y,theta):
x_new=x*cos(radians(theta))-y*sin(radians(theta))
y_new=x*sin(radians(theta))+y*cos(radians(theta))
return x_new,y_new
laserCuts_start_x_new=list(cut_pts_x)
laserCuts_start_y_new=list(cut_pts_y)
laserCuts_end_x_new=list(laser_cuts_x)
laserCuts_end_y_new=list(laser_cuts_y)
for i in range(1,5):
theta=i*72
for j in range(len(laser_cuts_x)):
x_1,y_1=rotate(cut_pts_x[j],cut_pts_y[j],theta)
x_2,y_2=rotate(laser_cuts_x[j],laser_cuts_y[j],theta)
laserCuts_start_x_new.append(x_1)
laserCuts_start_y_new.append(y_1)
laserCuts_end_x_new.append(x_2)
laserCuts_end_y_new.append(y_2)
#--- PLOTTING -----------------------------------------------------------------+
for i in range(len(laserCuts_start_x_new)):
x_new=[]
y_new=[]
x_new.append(laserCuts_start_x_new[i])
x_new.append(laserCuts_end_x_new[i])
y_new.append(laserCuts_start_y_new[i])
y_new.append(laserCuts_end_y_new[i])
plt.plot(x_new,y_new,'b',alpha=0.03,linewidth=4)
pentagon_pts.append(pentagon_pts[0])
x,y=zip(*pentagon_pts)
plt.plot(x,y,'k') # plot pentagon outline
plt.plot(0,0,'ro',markersize=3) # plot point at origin
plt.axes().set_aspect('equal')
plt.xlim([-1.1,1.1])
plt.ylim([-1.1,1.1])
##plt.savefig('06-final.png',dpi=72)
plt.show()
#--- END ----------------------------------------------------------------------+
Update: 2016-July-17
Holy shit, I won!

Additionally, I added the code to my GitHub which can be download (here).