Particle Swarm Optimization from Scratch with Python

Particle swarm optimization (PSO) is one of those rare tools that’s comically simple to code and implement while producing bizarrely good results. Developed in 1995 by Eberhart and Kennedy, PSO is a biologically inspired optimization routine designed to mimic birds flocking or fish schooling. I’ll occasionally use PSO for CFD based aerodynamic shape optimization, but more often than not, it’s for a machine learning project. PSO is not guaranteed to find the global minimum, but it does a solid job in challenging, high dimensional, non-convex, non-continuous environments. In this short introductory tutorial, I’ll demonstrate PSO in its absolute simplest form. At a later date, I’ll create another PSO tutorial featuring a more advanced implementation.

Below, are the only two equations that make up a bare bones PSO algorithm. As a heads up, “k” references the current iteration, therefore “k+1″ implies the next iteration.

Particle position:

$$ x_{k+1}^i = x_{k}^i + v_{k+1}^i $$

Particle velocity:

$$ v_{k+1}^i = w_k v_k^i + c_1 r_1 \left(p_k^i - x_k^i\right) + c_2 r_2 \left(p_k^g - x_k^i\right) $$

Where:

Variable	Definition
$$ x_k^i $$	particle position
$$ v_k^i $$	particle position
$$ p_k^i $$	best individual particle position
$$ p_k^g $$	best swarm position
$$ w_k $$	constant inertia weight
$$ c_1, c_2 $$	cognitive and social parameters respectively
$$ r_1, r_2 $$	random numbers between 0 and 1

From the particle velocity equation, two important groups emerge:

social term: $$ c_2 r_2 \left(p_k^g - x_k^i\right) $$
cognitive term: $$ c_1 r_1 \left(p_k^i - x_k^i\right) $$

Using these two simple equations, the basic flow structure of a PSO routine is as follows:

A) Initialize

Set constants: $$ k_{max}, w_k, c_1, c_2 $$
Randomly initialize particle positions.
Randomly initialize particle velocities.
Set k=1 (iteration counter).

B) Optimize

Evaluate cost function $$ f_k^i $$ at each particle position $$ x_k^i $$
If $$ f_k^i \le f_{best}^i $$ then $$ f_{best}^i = f_k^i $$ and $$ p_k^i = x_k^i $$.
If $$ f_k^i \le f_{best}^g $$ then $$ f_{best}^g = f_k^i $$ and $$ p_k^g = x_k^i $$.
If stopping condition is satisfied, go to C.
Update all particle velocities.
Update all particle positions.
Increment k.
Go to B(1).

C) Terminate

That’s it! It’s really that simple. The main concept behind PSO, which is evident from the particle velocity equation above, is that there is a constant balance between three distinct forces pulling on each particle:

The particles previous velocity (inertia)
Distance from the individual particles’ best known position (cognitive force)
Distance from the swarms best known position (social force)

These three forces are then weighted by $$ w_k $$, $$ c_1 $$, $$ c_2 $$ and randomly perturbed by $$ r_1 $$ and $$ r_2 $$. Thus depending on the weighting, either the swarms best location $$ p_k^g $$ or the particles own best position $$ p_k^i $$ will pull harder on the particle and dictate the overall direction. That’s assuming the particles initial velocity (or inertia) won’t cause the particle to wonder around. Often times, if you notice that the convergence is taking longer it’s because the particle inertia is weighted to heavily and should be reduced to speed up convergence. Keep in mind, that particle inertia is a double-edged-sword. If you’re dealing with a noisy, highly multimodal cost function, too little inertia could result in the particles getting trapped at a local minimum, unable to climb out.

In vector form, these three forces can be seen below (vector magnitude represents the weight value of that specific force):

Figure 1: a high energy particle that will keep exploring the search space

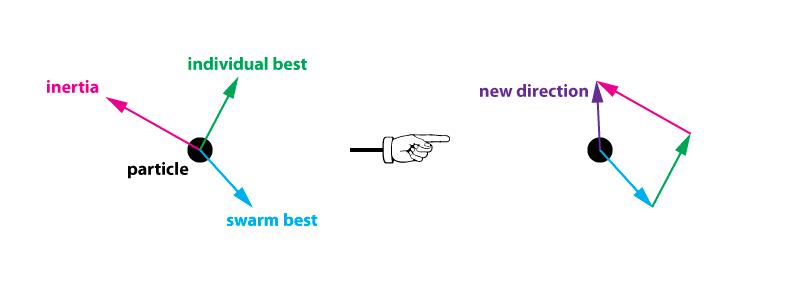
We can see in the above example that the weighting of the particles inertia and individual best overpower the swarms influence. In this scenario, the particle will continue exploring the search space rather than converge on the swarm. As another example below:

Figure 2: a lazy particle that follows the herd

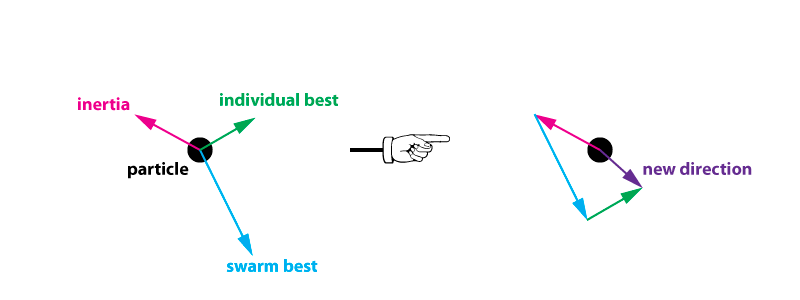
This time, the weighting assigned to the swarms influence overpowers the individual forces of the particle forcing it towards the swarm. This will result in a faster convergence, at the expense of not fully exploring the search space and potentially finding a better solution.

The implementation of a simple PSO routine in python is fairly straightforward. We are going to utilize some object-oriented programming and create a swarm of particles using a particle class. These particles will be monitored by a main optimization class. Below is the entire code:

#------------------------------------------------------------------------------+
#
#   Nathan A. Rooy
#   Simple Particle Swarm Optimization (PSO) with Python
#   July, 2016
#
#------------------------------------------------------------------------------+

#--- IMPORT DEPENDENCIES ------------------------------------------------------+

from __future__ import division
import random
import math

#--- COST FUNCTION ------------------------------------------------------------+

# function we are attempting to optimize (minimize)
def func1(x):
    total=0
    for i in range(len(x)):
        total+=x[i]**2
    return total

#--- MAIN ---------------------------------------------------------------------+

class Particle:
    def __init__(self,x0):
        self.position_i=[]          # particle position
        self.velocity_i=[]          # particle velocity
        self.pos_best_i=[]          # best position individual
        self.err_best_i=-1          # best error individual
        self.err_i=-1               # error individual

        for i in range(0,num_dimensions):
            self.velocity_i.append(random.uniform(-1,1))
            self.position_i.append(x0[i])

    # evaluate current fitness
    def evaluate(self,costFunc):
        self.err_i=costFunc(self.position_i)

        # check to see if the current position is an individual best
        if self.err_i < self.err_best_i or self.err_best_i==-1:
            self.pos_best_i=self.position_i
            self.err_best_i=self.err_i

    # update new particle velocity
    def update_velocity(self,pos_best_g):
        w=0.5       # constant inertia weight (how much to weigh the previous velocity)
        c1=1        # cognative constant
        c2=2        # social constant

        for i in range(0,num_dimensions):
            r1=random.random()
            r2=random.random()

            vel_cognitive=c1*r1*(self.pos_best_i[i]-self.position_i[i])
            vel_social=c2*r2*(pos_best_g[i]-self.position_i[i])
            self.velocity_i[i]=w*self.velocity_i[i]+vel_cognitive+vel_social

    # update the particle position based off new velocity updates
    def update_position(self,bounds):
        for i in range(0,num_dimensions):
            self.position_i[i]=self.position_i[i]+self.velocity_i[i]

            # adjust maximum position if necessary
            if self.position_i[i]>bounds[i][1]:
                self.position_i[i]=bounds[i][1]

            # adjust minimum position if neseccary
            if self.position_i[i] < bounds[i][0]:
                self.position_i[i]=bounds[i][0]
                
class PSO():
    def __init__(self,costFunc,x0,bounds,num_particles,maxiter):
        global num_dimensions

        num_dimensions=len(x0)
        err_best_g=-1                   # best error for group
        pos_best_g=[]                   # best position for group

        # establish the swarm
        swarm=[]
        for i in range(0,num_particles):
            swarm.append(Particle(x0))

        # begin optimization loop
        i=0
        while i < maxiter:
            #print i,err_best_g
            # cycle through particles in swarm and evaluate fitness
            for j in range(0,num_particles):
                swarm[j].evaluate(costFunc)

                # determine if current particle is the best (globally)
                if swarm[j].err_i < err_best_g or err_best_g == -1:
                    pos_best_g=list(swarm[j].position_i)
                    err_best_g=float(swarm[j].err_i)

            # cycle through swarm and update velocities and position
            for j in range(0,num_particles):
                swarm[j].update_velocity(pos_best_g)
                swarm[j].update_position(bounds)
            i+=1

        # print final results
        print 'FINAL:'
        print pos_best_g
        print err_best_g

if __name__ == "__PSO__":
    main()

#--- RUN ----------------------------------------------------------------------+

initial=[5,5]               # initial starting location [x1,x2...]
bounds=[(-10,10),(-10,10)]  # input bounds [(x1_min,x1_max),(x2_min,x2_max)...]
PSO(func1,initial,bounds,num_particles=15,maxiter=30)

#--- END ----------------------------------------------------------------------+

I hope this was helpful! If you want, you can download the entire code from my GitHub (here). Check back later for my post on a more advanced particle swarm optimization routine.