Effective Simulated Annealing with Python
Introduction
I use some form of optimization on a daily basis, whether it’s for work or personal projects. Something else I do on a daily basis is avoid simulated annealing. I’ve always associated simulated annealing with inefficiency. Yes, it’s a global optimizer, but at what cost? In most situations I’ve been able to achieve optimal or near-optimal results in a substantially quicker time using various other methods (particle swarm, genetic/evolutionary, etc…). So what’s the deal?
Over the winter I decided to invest some time in actually understanding this method and forced myself into using it. I learned a lot and actually use it from time to time now. I decided to document my learnings in the form of this tutorial to my future self and anyone else interested in simulated annealing.
Background
Simulated annealing is a probabilistic optimization scheme which guarantees convergence to the global minimum given sufficient run time. It’s loosely based on the idea of a metallurgical annealing in which a metal is heated beyond its critical temperature and cooled according to a specific schedule until it reaches its minimum energy state. This controlled cooling regiment results in unique material properties useful for specific applications.
At its core, simulated annealing is based on equation [1] which represents the probability of jumping to the next energy level. Within the context of simulated annealing, energy level is simply the current value of whatever function that’s being optimized.
$$ P(e_c, e_n, T) = e^{-\Delta E/T} \tag{1} $$
Nomenclature:
| $$ e_c $$ | energy at current state | |
| $$ e_n $$ | energy at proposed neighbor site | |
| $$ \Delta E $$ | change in energy between current state and proposed neighbor state | |
| $$ T $$ | current system temperature |
The main loop for simulated annealing consists of generating neighbor candidates which are just potential solutions which are then randomly accepted based on an ever increasingly more stringent threshold (Equation [1]).
0) # initialize
t_current = t_start
s_current = x0
s_best = x0
1) # main optimization loop
while t_current > t_min
1.A) generate neighbor candidate -> s_new
1.B) if P(E(s_current), E(s_new), T) >= random(0,1)
s_current = s_new
1.C) if E(s_new) < E(s_best)
s_best = s_new
1.D) update t_current
2) # end
output results
Although these equations appear simple, there’s actually a few interesting things going on. To point out the obvious, ΔE is positive for any transition resulting in a drop in energy (cost function improvement). Therefor the probability of accepting a lower energy state is 100%, while accepting a worse energy state is a non-zero value that depends on the size of the energy increase and the current system temperature. This also means that the ability to jump to a worse energy level is a very real possibility (which is actually a good thing).
When the annealing process first begins, the temperature is high and the acceptance criteria for a new neighbor candidate is relaxed. This means the peaks and valleys of the energy landscape are largely ignored resulting in a process not unlike a random walk. Bouncing aimlessly between high and low energy levels might seem counterproductive, however there is a method to this madness. It’s this erratic behavior that drives exploration of the search space, thus enabling it to find the global minimum. As the temperature is slowly cooled the acceptance criteria begins to narrow and the likelihood of transitioning to a neighbor candidate with a larger energy difference drops. At this point, simulated annealing is acting in a way which resembles stochastic gradient decent. The focus is centered around improvements rather than exploration and will generally follow a path of constant decent but may still jump around. As the system approaches its minimum energy state, only the smallest deviations in energy are accepted. This behavior is analogous to gradient decent in that it’s limited to just the local search space and driven entirely by solution improvement.
| temperature | approx. method | mode |
|---|---|---|
| high | random walk | global exploration |
| med | stochastic gradient decent | improvement focused |
| low | gradient decent | local search / exploit |
Balancing the transition phase between a global optimizer exploring the search space and a local optimizer exploiting only what’s in front is critical to achieving good results with simulated annealing. Using an aggressive cooling schedule on a highly multi-modal energy landscape can result in a solution frozen into a local minima, unable to escape to a lower energy level further away. Using a slower cooling schedule, will reduce the chances of getting trapped at the expense of increased computational requirements.
The simplicity of simulated annealing becomes further evident from its implementation in code below:
# begin optimizing
self.step, self.accept = 1, 0
while self.step < self.step_max and self.t >= self.t_min:
# get neighbor
proposed_neighbor = self.get_neighbor()
# check energy level of neighbor
E_n = self.cost_func(proposed_neighbor)
dE = E_n - self.current_energy
# determine if we should accept the current neighbor
if random() < self.safe_exp(-dE / self.t):
self.current_energy = E_n
self.current_state = proposed_neighbor[:]
self.accept += 1
# check if the current neighbor is best solution so far
if E_n < self.best_energy:
self.best_energy = E_n
self.best_state = proposed_neighbor[:]
# update some stuff
self.t = self.update_t(self.step)
self.step += 1
Throughout this tutorial, the code examples shown represent the bulk of the important stuff. I did however omit some methods, and non-critical code in the interest of readability. The full code can be viewed [here] or easily installed via the following:
pip install git+https://github.com/nathanrooy/simulated-annealing
Additionally, the example cases in the form of Jupyter notebooks can be found [here]
Implementation - Combinatorial
What better way to start experimenting with simulated annealing than with the combinatorial classic: the traveling salesman problem (TSP). After all, SA was literally created to solve this problem.
The first thing we need to sort out is how we’ll generate neighbor candidates. Luckily for combinatorial problems such as TSP, this is super easy. Given the current_state at iteration i, which is nothing more than a list of values representing nodes in the salesman’s path, we’re going to randomly swap two of them. Since this will be contained within the main minimize class, this becomes a simple method we’ll call move_combinatorial and can be seen below.
def move_combinatorial(self):
'''
Swaps two random nodes along a path
'''
p0 = randint(0, len(self.current_state)-1)
p1 = randint(0, len(self.current_state)-1)
neighbor = self.current_state[:]
neighbor[p0], neighbor[p1] = neighbor[p1], neighbor[p0]
return neighbor
Now that we have a way of generating neighbor candidates, we need to code out the actual TSP cost function. I went ahead and implemented the simplest version which utilizes a Euclidean distance metric calc_euclidean. This could very easily be swapped out for something else such as Haversine or Vincenty (both available here) if the nodes were instead specified as values of latitude and longitude.
def calc_euclidean(p1, p2):
return ((p1[0] - p2[0])**2 + (p1[1] - p2[1])**2)**0.5
The main tsp class is as simple as it sounds:
class tsp():
def __init__(self, dist_func, close_loop=True):
self.dist_func = dist_func
self.close_loop = close_loop
def dist(self, xy):
# sequentially calculate distance between all tsp nodes
dist = 0
for i in range(len(xy)-1):
dist += self.dist_func(xy[i+1], xy[i])
# close the tsp loop by calculating the distance
# between the first and last points
if self.close_loop:
dist += self.dist_func(xy[0], xy[-1])
return dist
The tsp cost function can then be initialized in the following way:
tsp_dist = tsp(dist_func=calc_euclidean, close_loop=True).dist
In the interest of keeping it simple while starting out, let’s create a tsp path in the shape of a circle. Since we know the optimal solution will follow the perimeter, it will be easy to validate.
n_pts = 10
dr = (2 * pi) / n_pts
x0 = []
for i in range(0,n_pts):
radians = dr * i
x0.append([cos(radians), sin(radians)])
shuffle(x0)
With 10 points, the optimal energy (path length in this case) is ~6.1803 (just under 2π) but jumps to 15.3540 because of the random shuffle. Now, everything is in place and we can begin optimizing.
opt = sa.minimize(
tsp_dist,
x0,
opt_mode='combinatorial',
step_max=750,
t_max=4,
t_min=0)
Once finished, we can view the results by calling the results() method:
opt.results()
Which will yield the following (usually):
+------------------------ RESULTS -------------------------+
cooling sched.: linear
opt.mode: combinatorial
initial temp: 4
final temp: 0.000000
max steps: 750
final step: 750
final energy: 6.180340
+-------------------------- END ---------------------------+
We can access the optimal solution via:
opt.best_state
And then plot it to further validate that we have indeed achieved the global minimum.
In order to get a better understanding of how simulated annealing converges onto the solution for this example, I went ahead and ran it 1000 times and consolidated the results into the mean and 90% confidence intervals. The first plot below shows the current state of the optimizer. We can see that it quickly accrues some easy wins before settling ito a gently descending trajectory. We can also see that towards the end of the run, the confidence interval begins to shrink indicating a temperature level which prioritizes local improvements over exploration.
The last plot below, shows the best solution achieved throughout the optimization process. We can see that early on, simulated annealing is able to quickly capture the low hanging fruit during the exploration phase. After the quick gains, progress slows while it continues to search the energy landscape until finally converging on the optimal solution.
Okay I can’t resist, lets swap out that distance function for something a little more fun/useful. Let’s say we want to bike to every one of our favorite breweries in Cincinnati in the shortest distance possible (this is what initially piqued my interest in simulated annealing 🚴♂️🍺). In this situation, since we’re limited to streets and bike paths we’ll need to use network distance. However, since network distance relies on Dijkstra’s algorithm to find the shortest path between two nodes in a graph, it requires more compute power than the simpler Euclidean distance. We could keep it simple by coding out Dijkstra’s algorithm and pairing that with the OpenStreetMap network graph but we’d be stuck calling the function a bunch of times for the same set of points. This is both lazy and inefficient. Instead, let’s enumerate all origin-destination pairs and pre-compute the distances. We can then save the results in the form of a distance matrix which will act as a sort of lookup table allowing for super quick function calls. This results in a new distance function as seen below:
def calc_dict(p1, p2, dist_dict=dist_dict):
return dist_dict[p1,p2]
Which we can then use to initialize the updated tsp cost function:
tsp_bike = tsp(dist_func=calc_dict, close_loop=True).dist
Just as before, we’ll call the minimize method from our simulated annealing class to begin the optimization.
opt = sa.minimize(
tsp_bike,
x0,
opt_mode='combinatorial',
step_max=1000,
t_max=50,
t_min=0)
Since the breweries are listed in an arbitrary order, the initial energy of the system is roughly 84481.27 which represents the total circuit length in meters (52.49 miles). Below is the initial state (red dots indicate brewery locations while the red line is the travel path):
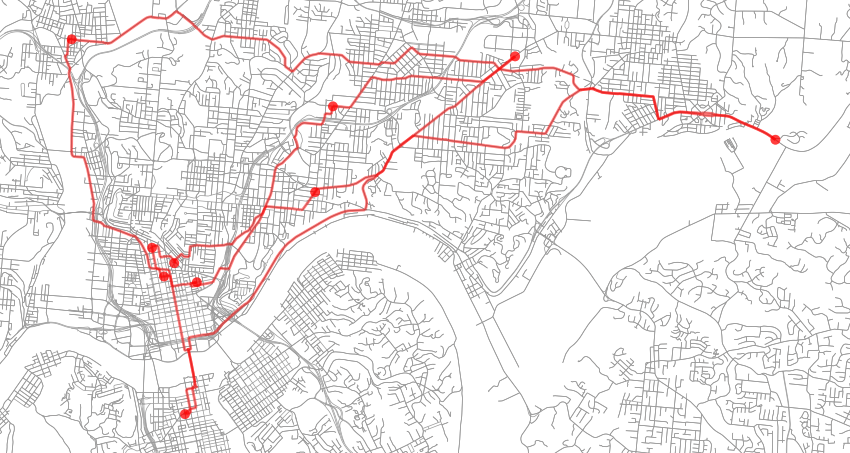
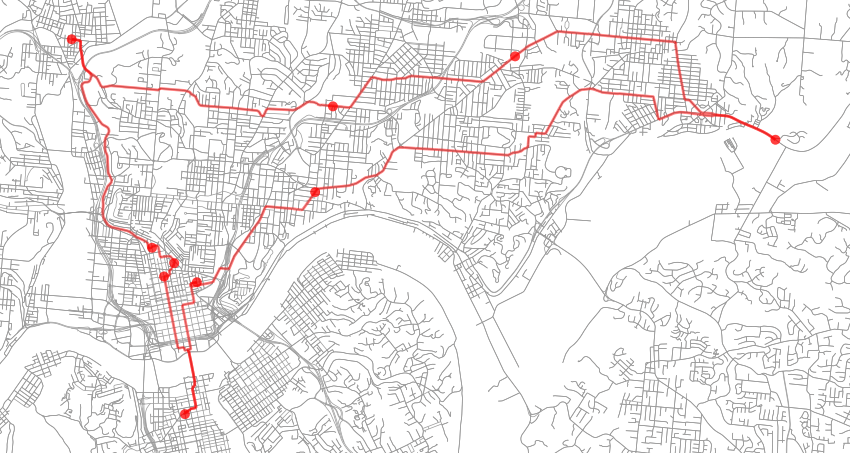
After optimization, the final state has an energy of roughly 51104.00 (31.75 miles) and can be seen below. I ran this example several times with varying levels of t_max, t_min and max_iters and they all converged to the same solution the majority of the time indicating that the energy landscape for this case is multi-modal but fairly smooth.
Implementation - Continuous
Now for the fun stuff; continuous real valued problems! Let’s say you’re an engineer working within Lockheed Skunk Works and aerospace legend Kelly Johnson stops by your desk and requests an airfoil for a new high altitude reconnaissance aircraft code named Dragon Lady.1 You’ve got access to the best compute resources the 1950’s has to offer and one day. Time is ticking.

Ignoring the vast majority of constraints that are usually at play in a situation such as this, we’re going to instead focus on a single objective: maximizing the ratio of lift to drag. For this, we’ll start with the NACA 0012. This is a symmetric airfoil which means it has no camber and subsequently generates no lift when the angle of attack (α) is at zero degrees. This will provide a neutral starting point for this exercise.
The symmetric NACA 4-digit airfoils are described using a simple formula which is based on the ratio of maximum thickness to chord length. This is great because it’s simple and easy to implement, but terrible for optimization. How are we going to meaningfully change the shape of the airfoil if we only have this single ratio? Sure, we could use a more advanced NACA formulation but in the end, we’re still going to limit ourselves. Instead, let’s parameterize our airfoil using Bézier curves. Because this is a tutorial on simulated annealing and not aerodynamic shape optimization, I’ll spare all the juicy details for another day.
Long story short, the airfoil has been converted from a series of points into a parametric curve through the use of a composite quadratic Bézier curve (more on that here). What this means, is that we can now morph the shape of this airfoil using a series of control points to generate an infinite number of different variations. Perfect for optimization.
As seen from above, the airfoil has been parameterized with 10 control points, however the two at the trailing edge are fixed and the two leading edge control points can only move along the y-axis. The rest can move freely in both the x, and y directions. What this means is that we have a system with 13 degrees of freedom which is plenty enough for this task. Adding more control points would enable a higher level of fidelity but at the expense of a larger search space making optimization a more difficult.
Now that we have a parameterized airfoil we need to two more things: a way of generating neighbor candidates and a cost function. The neighbor generation for this example will remain simple, let’s just randomly perturb each control point by a small random amount. In code, this looks like this:
def move_continuous(self):
# perturb current state by a random amount limited by the damping factor
neighbor = []
for item in self.current_state:
neighbor.append(item + ((random() - 0.5) * self.damping))
# clip to upper and lower bounds
if self.bounds:
for i in range(len(neighbor)):
x_min, x_max = self.bounds[i]
neighbor[i] = min(max(neighbor[i], x_min), x_max)
return neighbor
Note, that I added a simple check that forces the new neighbor candidate to remain within some bounds as optionally specified by the user. Lastly, the cost function consists of nothing more than creating the new airfoil, calculating the aerodynamic forces, and returning the results. Aerodynamic forces will be calculated using XFOIL which is based on a linear-strength vortex panel method.2,3 Given the time period and compute limitations, panel methods would have been the likely approach taken rather than a CFD based approach.
def cost_function(x, x_coords=x_cos):
airfoil_file = 'airfoil.txt'
try:
# munge x-vector into bezier format
control_pts = munge_ctlpts(x)
# generate new airfoil
curve = bezier_airfoil(x_coords, control_pts)
# output airfoil to csv
with open(airfoil_file,'w') as out_file:
out_file.write('x,y\n')
for item in curve:
out_file.write(f'{item[0]},{item[1]}\n')
# run xfoil and collect results
results_dict = run_xfoil()
# determine cost
cost = results_dict['cl'] / results_dict['cd']
if results_dict['cl'] < 0: cost = 0.01
except:
cost = 0.01
# remove temp airfoil file
os.system(f'rm -rf {airfoil_file}')
return 1000.0 / cost
Now, everything is in place and we can begin optimizing (reference the jupyter notebook [here] for all the details).
opt = sa.minimize(
cost_function,
x0,
opt_mode='continuous',
step_max=125,
t_max=2,
t_min=0,
damping=0.01
)
Because the initial reverse-fitting yielded an airfoil that wasn’t perfectly symmetrical, the initial L/D was slightly less than 0.5, while the optimized airfoil achieved an L/D of just over 100. While running this example, it’s fairly common to get an airfoil with an L/D nearing 200 however these tend to be structurally unfeasible and suffer from highly unfavorable stability characteristics. So what you see below is actually not a global optimum but a slightly more realistic local optimum.
Given that XFOIL is able to calculate all useful aerodynamic forces, it would be trivial to incorporate additional constraints such as stability or lift across a range of Reynolds numbers.
Cooling Schedules
The concept of a cooling schedule is a big part of simulated annealing and until now I’ve purposely left out how temperature reduction actually occurs. They come in a number of different flavors and the choice of which cooling schedule to use is considered an important decision.4 There exists a whole body of research on cooling schedules each with their own advantages and disadvantages. Some such as multiplicative monotonic cooling schedules rely on nothing more than the starting temperature (T_max), the current step (k), and a manually set constant alpha.
linear multiplicative
$$ T(k) = T_{max} - \alpha k \tag{3} $$ natural log exponential multiplicative
$$ T(k) = T_{max} \alpha^{k} \tag{4} $$
logarithmic multiplicative
$$ T(k) = \frac{T_{max}}{1 + \alpha log(k+1)} \tag{5} $$
quadratic multiplicative
$$ T(k) = \frac{T_{max}}{1 + \alpha k^2} \tag{6} $$
On the other hand, additive monotonic cooling schedules depend on two additional parameters: the total number of steps n and the final temperature (t_min).
linear additive:
$$ T(k) = T_{min} + (T_{max} - T_{min}) \left( \frac{n - k}{n} \right) \tag{7} $$
exponential additive:
$$ T(k) = T_{min} + (T_{max} - T_{min}) \left( \frac{1}{1+e^{\frac{2 \ln (T_{max}-T_{min})}{n} \left(k-\frac{1}{2}n \right)}} \right) \tag{8} $$
quadratic additive:
$$ T(k) = T_{min} + (T_{max} - T_{min}) \left( \frac{n - k}{n} \right)^2 \tag{9} $$
Lastly, we have the non-monotonic adaptive cooling schedules which involve all previously mentioned parameters as well as an adaptive factor based on the difference between the current state and the best state achieved thus far.
$$ T(k) = \mu T_k $$
Where:
$$ \mu = \left [1 + \frac{e_c - e_{best}}{e_c} \right] $$
and T_k is the temperature at step k using any one of the previous methods. Also, e_c is the energy at the current step, and e_best is the best energy state achieved thus far.
All these approaches are useful, but of particular interest are the multiplicative and additive cooling schedules. Cooling schedules in general are fairly simple, but these are the simplest. Throughout this entire tutorial, a linear additive cooling schedule has been used and from my experience, will always deliver decent results.
As you might expect, the cooling schedule names are fairly indicative of how they behave. Upon visualization, it’s interesting to see how these cooling schedules differ from each other. We can see that the linear approach favors both exploration and exploitation equally where as the exponential and logarithmic schemes force the transition into exploit mode much sooner.
All of these cooling schedules are available in the current implementation. As an example, if we wanted the linear additive cooling schedule, we just need to specify it as follows:
sa.minimize(cost_func, x0, cooling_schedule='linear')
By not specifying a value for alpha, the cooling schedule will default to the additive scheme. In the event that the multiplicative version of linear cooling is required, just specify a value for alpha.
sa.minimize(cost_func, x0, cooling_schedule='linear', alpha=0.8)
Tips on Using SA Effectively
This last section here is comprised of what I’ve learned to be most helpful when using simulated annealing. Given that SA only requires a few parameters, it’s important that we do our best to set them accordingly. Doing so will increase the likelihood of obtaining the optimal solution.
cooling schedule: If we know our cost function is smooth and unimodal or nearly unimodal, then don’t waste excess time exploring the search space. Instead, force the transition to gradient decent sooner rather than later with a logarithmic or exponential cooling schedule. On the other hand, if the cost function is highly multi-modal and an investment in exploration is warranted, go with the linear or quadratic cooling schedules. If you’re unsure, keep it simple and go with the linear schedule.
initial temperature: Depending on how expensive the cost function is in terms of compute requirements, one of the easiest ways to determine t_max is by running SA over a range of t_max values with a constant temperature while checking the acceptance rate (the rate at which neighbor candidates are accepted). By holding the temperature constant, we can easily determine which range of t_max values will give us our initial desired acceptance rate. Usually, an initial acceptance rate of 0.8 or greater is used.
One way to maintain a constant temperature during optimization is by using the linear cooling schedule with an alpha set to zero as follows:
sa.minimize(cost_func, x0, t_max=10, cooling_schedule='linear', alpha=0)
After completion, the acceptance rate can then be checked via:
sa.acceptance_rate
which can be persisted in memory and plotted like so:
We can see that with any initial temperature greater than about two, we’ll likely be wasting our time. For a more rigorous approach to calculating t_max see: Computing the Initial Temperature of Simulated Annealing.5
max steps: To state the obvious; more is better, …but only if you’re seeing improvements. One way to check if max_steps has been set correctly is by looking at how the solution converges.
step, temp, current_energy, best_energy = zip(*opt.hist)
If you plot these out and see that improvements become stagnate halfway through there’s a few possible routes you can take. If you’re confident in the cooling schedule choice and initial temperature, then max_iters can safely be reduced. If you’re not confident or you think you might be getting trapped in a local minima, better re-evaluate the initial temperature and cooling schedule.
Final Thoughts
Simulated annealing can be a tricky algorithm to get right, but once it’s dialed in it’s actually pretty good. It’s one of those situations in which preparation is greatly rewarded. It’s probably overkill for most applications, however there are those rare situations which demand something stronger than the usual methods and simulated annealing will gladly deliver. Hopefully by shedding some light on the inner workings of this very simple but powerful scheme, you may find yourself (just like I have) using it a little more often.
Lastly, if you find anything that wasn’t completely clear please reach out because odds are other people feel the same way. I hope this tutorial was helpful, thanks for reading!
- Nathan
Peter W. Merlin, Unlimited Horizons: Design and Development of the U-2 (NASA Aeronautics Book Series, 2015) ↩︎
Mark Drela, XFOIL: An Analysis and Design System for Low Reynolds Number Airfoils (MIT Dept. of Aeronautics and Astronautics, Cambridge, Massachusetts) ↩︎
Joseph Katz, Allen Plotkin, Low-Speed Aerodynamics (Cambridge University Press - 2001) ↩︎
Yaghout Nourani and Bjarne Andresen, A comparison of simulated annealing cooling strategies (Journal of Physics A: Mathematical and General Volume 31, Number 41. October 16, 1998) ↩︎
Walid Ben-Ameur, Computing the Initial Temperature of Simulated Annealing (Computational Optimization and Applications 29(3):369-385 - December 2004) ↩︎